暂且先不讨论CBC模式本身而言在密码学上的安全性。首先看为什么不能直接使用块加密例如：AES或者3DES之类的对保密性数据进行加密。

0x01为什么要使用CBC模式

暂且先不讨论CBC模式本身而言在密码学上的安全性。首先看为什么不能直接使用块加密例如：AES或者3DES之类的对保密性数据进行加密。

以AES为例，我们知道，对于长序列加密的时候，首先是分组成 128 bit，然后分别用给定的K进行加密。那么显然，对一般数据而言，如果两个分组恰巧值相同，那么加密结果必然相同，如果值不同，加密结果在很大的可能上不同。
具体可以看如下这个图片的数据加密前后的对比图：

CBC 模式加密前后对比图

图1：CBC 模式加密前后对比图

很显然，图片很直观地反映出了这种加密方式的弊端 —— 存在某种程度的信息“暴露”。图片加密之后依旧能依稀辨认出那是一张短头发人的照片。所以说，CBC加密模式应运而生。（实际上，没有采用计数器或者随机值介入，这种确定性加密在面对选择明文攻击的时候是不安全的)

0x02什么是CBC加密模式

这一点当然还是用图片最形象了：

CBC加密模式图解

图2：CBC 加密模式图解

可见，这个时候每一个分组在加密之前，都先与前一个分组密文结果进行异或，从而“打乱”原来的信息。而解密则是与其类似，只不过运算块变成了解密，且先解密后再与前一组密文异或，从而还原出明文。这样就避免了之前所提到的问题。但是，如果你仔细想一想就会发现，如果攻击者可以修改密文的话，那就会出现很大的问题。

具体如下图所示：

CBC-bit 反转攻击图解

图3：CBC-bit 反转攻击图解

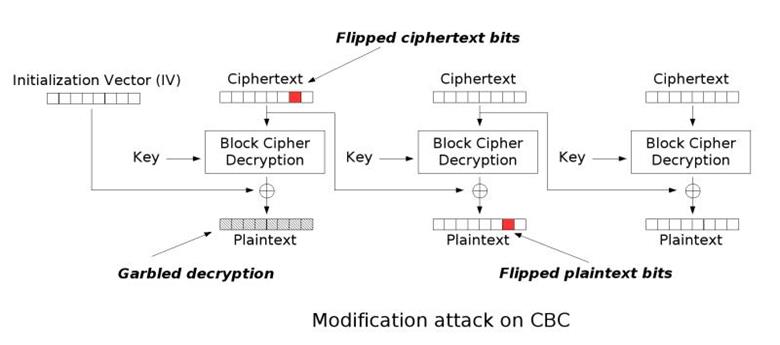
假设明文块序列用 $( P )$ 表示，密文块序列用 $( C )$ 表示（参看图2： CBC 加密模式图解），块分组运算出来（用来与前一分组的密文执行异或运算）的序列用 $( D )$ 表示（参看图3：CBC-bit 反转攻击图解），流程中可控的内容如 $( x )$ ，通过撇号标识为 $( x' )$ 以示区分，攻击思路如下：
　　
现假设要通过攻击改变的明文块为 $( P_{i+1}' )$

解密时很明显有（注意标识，参考上图红色标识）：

$$ P_{i+1}' = C_i' \oplus D_{i+1} $$

由加密过程已知（参看上面 CBC 加密模式图，块分组运算模块送入和送出的内容相同）：

$$ D_{i+1} = C_i \oplus P_{i+1} $$

由上两式子可得（同样，注意标识）：

$$ P_{i+1}' = C_i' \oplus C_i \oplus P_{i+1} $$

注意分辨 $( C_i )$ 与 $( C_i' )$ ，前者表示加密过程中该块的密文结果，后者通过撇号标识表示被攻击的解密过程中可控的密文块。当然，在正常情况下，没有受到攻击，两者相等，解密无误。

现在假设密文我们可以随意修改，即解密时密文块可控（这种假设是符合网络攻击时的具体情况的），那么，若将 $( C_i' )$ 修改为 $( W \oplus C_i )$ （回忆上述内容，撇号只是标识可控，这是敌手可以做到的），此时有：

$$ \begin{split} P_{i+1}' &= W \oplus C_i \oplus C_i \oplus P_{i+1} \\ &= W \oplus P_{i+1} \end{split} $$

由此可知，可以做到随意修改 $( P_{i+1}' )$ ，因为 $( W )$ 可以随便设。例如要把明文分组 $( P_{i+1} )$ 处的 $( A )$ 换成 $( B )$ ，那么，把 $( C_{i}' )$ 替换成 $( C_i \oplus A \oplus B )$ 即可。此时有：

$$ \begin{split} P_{i+1}' &= C_i \oplus A \oplus B \oplus C_i \oplus A \\ &= B \end{split} $$

可见，达到了攻击的效果。

0x03具体应用

上面说的自己都感觉复杂了，主要还是在于自己表述能力不行，其实仔细看图还是比较好理解的。 CBC 比特翻转攻击的具体应用也是有的，此刻时间比较晚了，再加上篇幅所限就不挤在这篇文章了，回头另外写一篇把链接贴过来。

Update：2015/11/15

之前说要写的具体应用例子已经写了，传送门： CBC比特翻转攻击应用实例